
AVL tree, 0, 10, 30, 20, 50, 80, 40, 90, 70, 60
1.
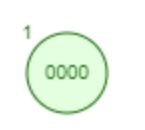
2.

3.
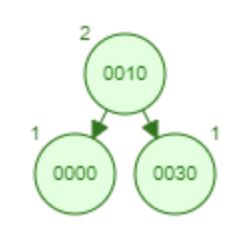
4.
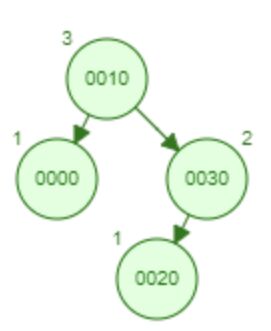
5.
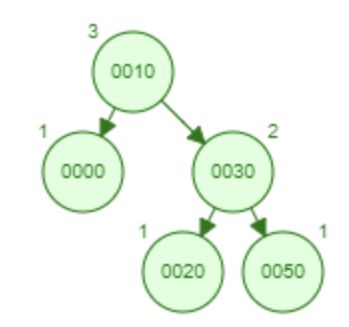
6.
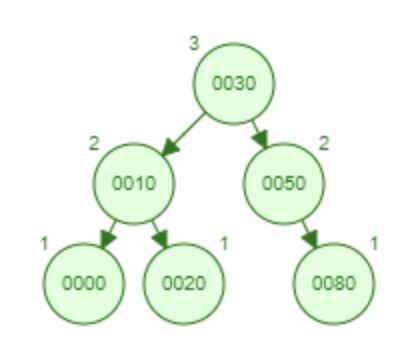
7.
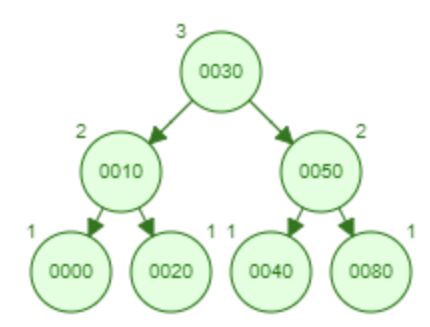
8.
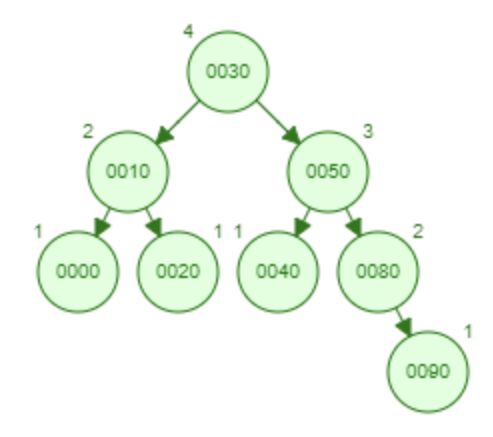
9.
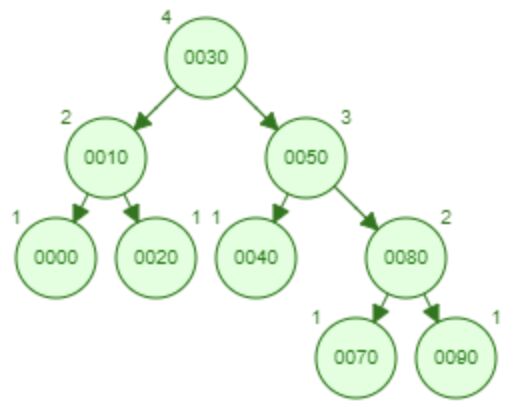
10.
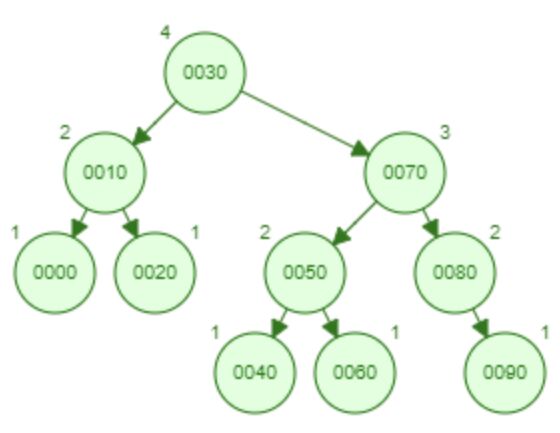
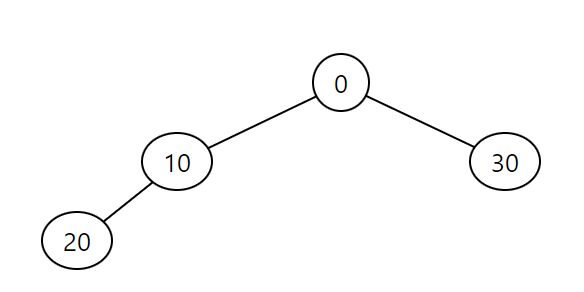
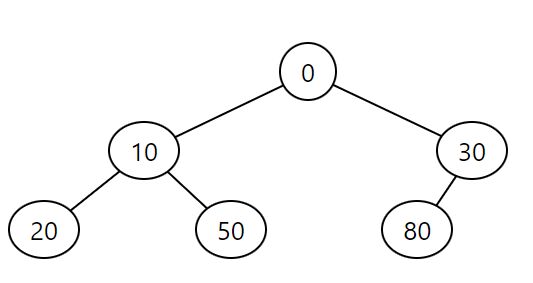
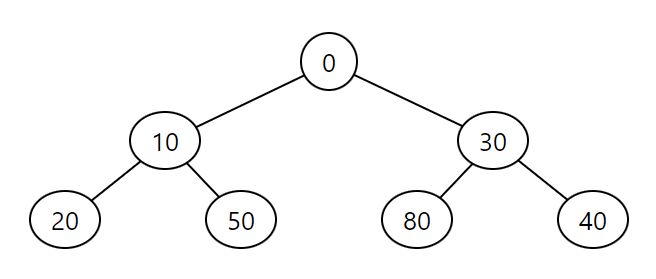
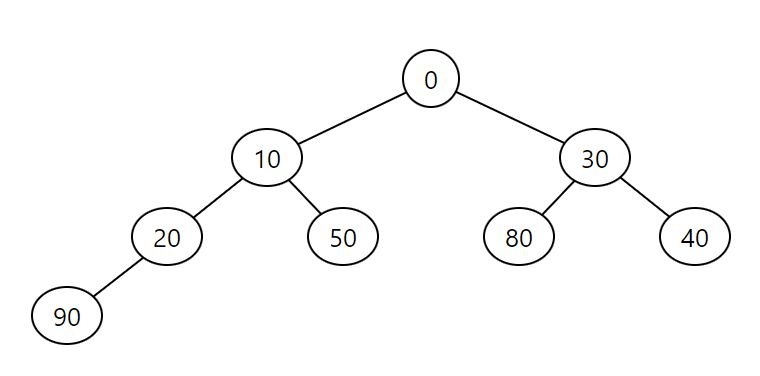
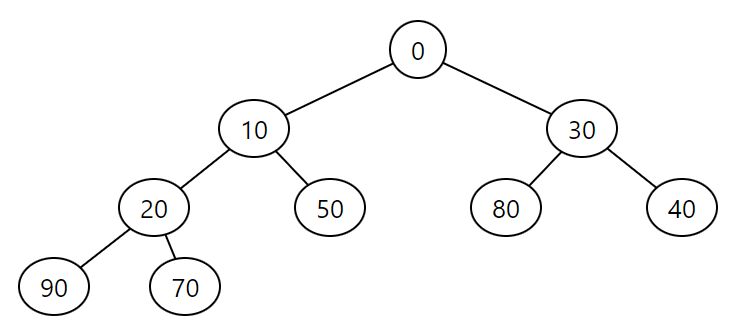
Min heap, 0, 10, 30, 20, 50, 80, 40, 90, 70, 60
1.
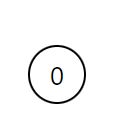
2.
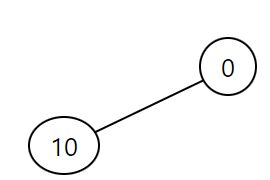
3.
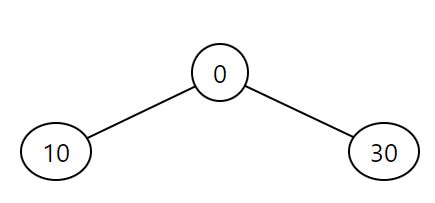
4.
5.

6.
7.
8.
9.
10.
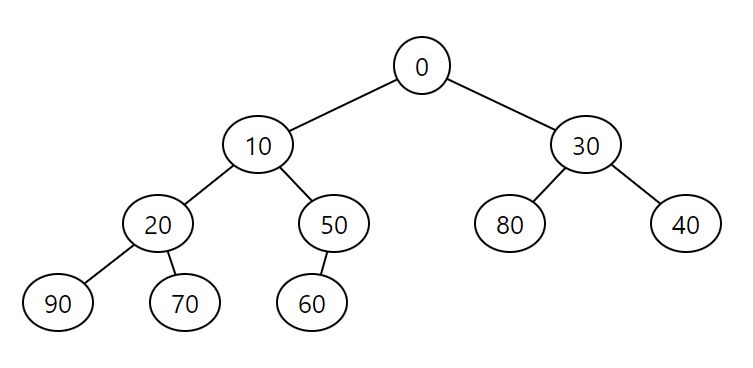
Max heap, 0, 10, 30, 20, 50, 80, 40, 90, 70, 60
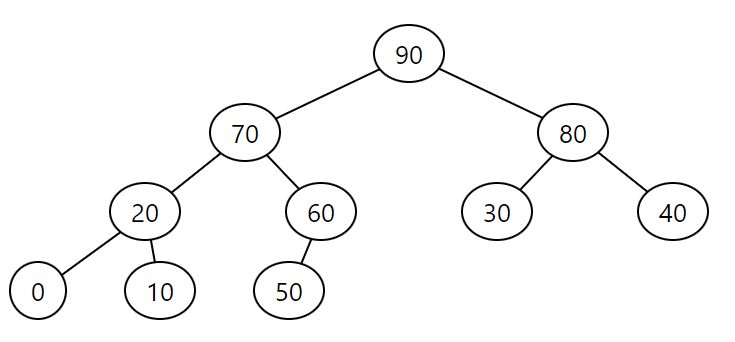
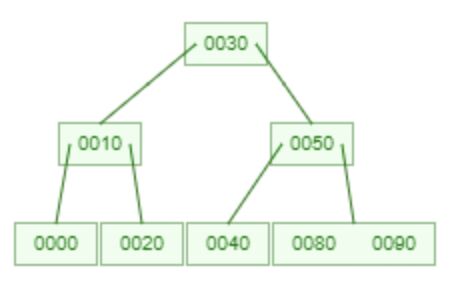
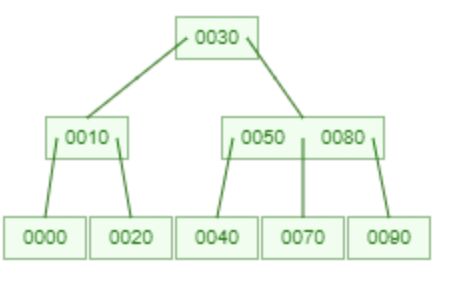
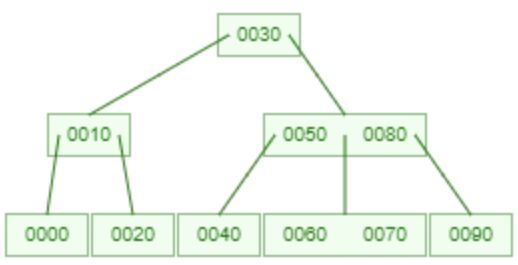
2-4 tree, 0, 10, 30, 20, 50, 80, 40, 90, 70, 60
1.

2.
3.
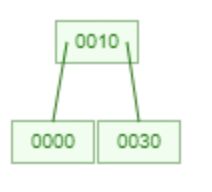
4.
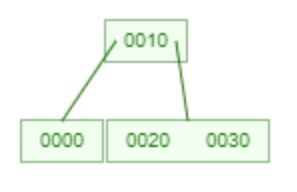
5.
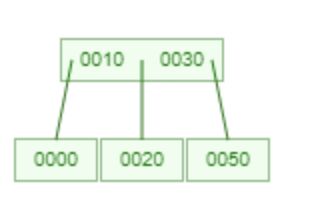
6.

7.
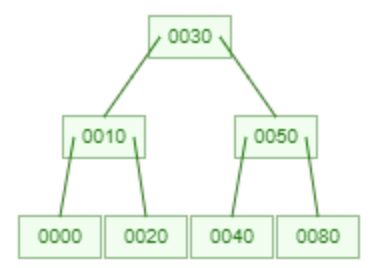
8.
9.
10.
AVL 樹、Min 樹、Max 樹和 2-4 樹是電腦科學中與樹狀資料結構相關的概念。讓我們討論每一個,以了解它們是否被視為平衡樹或搜尋樹。
1. AVL 樹
- 性質: 平衡二元搜尋樹 (BST)。
- 描述: AVL 樹是自平衡二元搜尋樹。樹中每個節點的左右子樹的高度差(稱為平衡因子)最多為 1。這種平衡確保了插入、刪除和搜尋等操作可以在 O(log n) 時間內完成,其中 n 是樹中的節點數。
2. Min 樹
- 性質: 這個詞彙在電腦科學中並不標準。然而,它可以指每個節點的值均小於或等於其子節點的值的樹。它通常與 Min 堆有關。
- 描述: 如果「Min 樹」是指 Min 堆,它是一個完全二元樹,其中每個節點的值均小於或等於其子節點。它通常用於優先隊列的實現。它不一定是平衡二元搜尋樹,而是一種專門的堆結構。
3. Max 樹
- 性質: 類似於 Min 樹,「Max 樹」不是一個標準詞彙。它可以指代 Max 堆。
- 描述: 如果是指 Max 堆,它是一個完全二元樹,其中每個節點的值大於或等於其子節點的值。與 Min 堆一樣,它不是平衡二元搜尋樹,而是各種演算法中使用的專門堆結構。
4. 2-4 樹
- 性質: 平衡搜尋樹。
- 描述: 2-4 樹是一種自平衡搜尋樹,其節點可以有 2、3 或 4 個子節點。每個葉節點具有相同的深度或層級,以確保樹保持平衡。2-4 樹中的所有操作,如插入、刪除和搜尋,都以 O(log n) 時間完成。
總結來說,AVL 樹和 2-4 樹都是平衡搜尋樹。它們維護平衡以確保可以有效地執行搜尋操作。另一方面,如果 Min 樹和 Max 樹是指 Min 堆和 Max 堆,它們通常不被視為平衡二元搜尋樹,而是用於特定應用程序(如優先隊列)的專門堆結構。它們更注重維護堆的屬性(最小或最大),而不是為了有效搜尋而平衡。
点点赞赏,手留余香
给TA打赏





評論0